Zadanie 1. 

Wyznacz sumę: 

Zadanie 2. 

Kierowca samochodu porusza się po torze wyścigowym z jednakową prędkością. Tor jest tak wyprofilowany, że nie można przekroczyć prędkości 200. Kierowca zauważył, że licznik przejechanych kilometrów wskazywał liczbę 13931, którą czyta się jednakowo w obie strony. Po upływie dokładnie 2 godzin licznik ponownie wskazywał liczbę o podanej wyżej własności. Z jaką prędkością poruszał się samochód w ciągu tych dwóch godzin?

Zadanie 3. 

Zakładamy, że Ziemia jest kulą. Ziemię opasano drutem wzdłuż równika tak, aby drut dokładnie przylegał do jej powierzchni. Następnie długość tego drutu zwiększono o 6,28 metra i podniesiono go na jednakową wysokość na całej długości. Czy pod tym drutem przejdzie lalka o wysokości 25 cm? Przyjmij, że 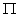= 3,14.

Zadanie 4. 

Zapalono dwie świece o różnych długościach i grubościach. Dłuższa z nich spala się zupełnie w ciągu 3 godzin, a krótsza
– w ciągu 5 godzin. Długości obu świec wyrównały się po dwóch godzinach palenia się tych świec. Ile razy jedna świeca była dłuższa od drugiej przed zapaleniem?

Zadanie 5. 

Dwa pociągi, z których każdy ma 40 wagonów, spotykają się na pojedynczym torze. Do tego toru dochodzi boczny tor, który może pomieścić lokomotywę i najwyżej 20 wagonów. W jaki sposób te pociągi mogą się wyminąć?

Zadanie 6. 

Do dwóch okręgów stycznych zewnętrznie poprowadzono wspólną styczną nieprzechodzącą przez ich punkt styczności. Oblicz pole figury zawartej między styczną i okręgami wiedząc, że promień jednego z nich ma długość 2 cm, a drugiego 6 cm.

Zadanie 7. 

Liczbę a, której odwrotność jest średnią arytmetyczną odwrotności dwóch danych liczb dodatnich b i c, nazywamy średnią harmoniczną liczb b i c.

1. Oblicz średnią harmoniczną liczb 5,5 oraz .

2. Wykaż, że iloczyn średniej arytmetycznej oraz średniej harmonicznej dwóch liczb dodatnich jest równy iloczynowi tych liczb.