Zadanie 1.
Wyraź 10 za pomocą pięciu dziewiątek. Podaj trzy różne sposoby. Uwaga: możesz używać znaków działań arytmetycznych.

Zadanie 2.
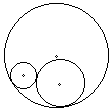
Dwa okręgi styczne zewnętrznie są równocześnie styczne wewnętrznie do trzeciego okręgu o promieniu długości 3 cm, tak jak na rysunku. Oblicz obwód trójkąta, którego wierzchołkami są środki tych okręgów.

Zadanie 3.
Spośród poniższych zdań, wskaż zdanie będące definicją rombu.

a) romb jest to czworokąt, który ma wszystkie boki równej długości,
b) romb jest to czworokąt, w którym przekątne są prostopadłe,
c) romb jest to równoległobok, w którym przekątne są prostopadłe,
d) romb jest to czworokąt, w którym są dwie pary kątów przystających.

Zadanie 4.
Znajdź resztę z dzielenia liczby 2⁹⁹ przez 3.

Zadanie 5.
Drewniany sześcian, którego wszystkie ściany są pomalowane na czerwono, został rozpiło-wany na 1000 przystających sześcianów. Ile jest sześcianów, które:

a) mają tylko 2 czerwona ściany,
b) mają tylko 1 czerwoną ścianę,
c) nie mają czerwonej ściany?

Zadanie 6.
Oblicz pole figury zakropkowanej na rysunku,
      
wiedząc, że |AB| = 2a, |BC| = a, gdzie a > 0 oraz E i F są środkami boków AB i CD prostokąta ABCD.

Zadanie 7.
Wśród dziewięciu monet znajduje się dokładnie jedna moneta fałszywa, która jest minimal-nie lżejsza od pozostałych. Iloma ważeniami, nie używając odważników, można wykryć monetę fałszywą, jeżeli do dyspozycji mamy wagę szalkową? Opisz przebieg ważenia.

Zadanie 8.
Dane są trójkąty o bokach długości:

a) 6, 8, 10,
b) 6, 8, 11,
c) 6, 8, 12.

Zadanie 9.
Odtwórz brakujące cyfry:

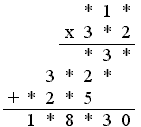
POWODZENIA!