|
Zadanie 1.
Odpowiedz (jeśli to możliwe), jaką miarę ma kąt x w figurach przedstawionych na rysunku. Odpowiedź uzasadnij.
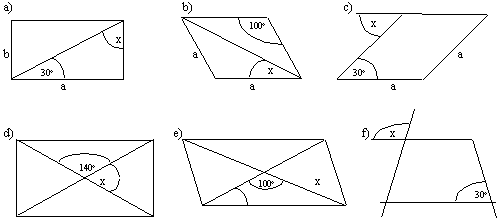
Uwaga: Jeśli chcesz wprowadzić oznaczenia, to możesz w czystopisie sporządzić rysunek pomocniczy (bez użycia przyrządów).
Zadanie 2.
Sweter podrożał o 10% i osiągnął taką samą cenę, jak kurtka, która właśnie staniała o 20%, a której poprzednia cena wynosiła 99 zł. Jaka była różnica cen kurtki i swetra przed zmianami cen?
Zadanie 3.
Narysuj trójkąt prostokątny równoramienny o przyprostokątnych równych 4. Wpisz w niego okrąg i opisz na nim okrąg. Oblicz odległość między środkami tych okręgów.
Zadanie 4.
W pewnej grupie uczniów średnia wieku wynosi 11 lat. Najstarszy z nich ma 17 lat, a śred-nia wieku wszystkich pozostałych wynosi 10 lat. Ilu uczniów liczy ta grupa?
Zadanie 5.
Podziel poniższy trapez prostokątny na cztery jednakowe (przystające) części.

Zadanie 6.
Dwóch zawodników ściga się na dystansie 100 m. Wygrywa A, z przewagą 10 metrów. Aby wyrównać szanse, w następnym wyścigu A staje 10 metrów przed linią startu, tym samym dając B 10 metrów forów. Odbywa się drugi wyścig, w którym obydwaj biegną z dokładnie taką samą prędkością jak poprzednio. Kto wygra? Odpowiedź uzasadnij.
Zadanie 7.
Dane są niezerowe odcinki o długościach a i b. Skonstruuj odcinek o długości x taki, że:
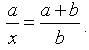
Zadanie 8.
Na jednym z bazarów Swarzędza, ceny wszystkich artykułów są liczbami naturalnymi. Dziś ma miejsce sprzedaż promocyjna pod hasłem "wszystko po 10 zł". Dla "złagodzenia" nieza-dowolenia niektórych klientów, dyrektor bazaru wprowadza dodatkowo zasadę: każdy klient, który kupi co najmniej 2 artykuły tego samego rodzaju, sprzedawane dotychczas po mniej niż 10 zł, zapłaci za nie nową cenę pomniejszoną o dotychczasową wartość jednego z nich. Nie zważając na ceny, pani Kowalska kupiła kilka srebrnych widelców. Okazało się, że zapłaciła dokładnie tę samą kwotę, którą zapłaciłaby przed zmianą cen. Jaka była cena widelca przed zmianą cen?
POWODZENIA!
|

![]](themes/crookedgreen/images/whiter.gif)
 v6.00.203 © 2003-2005
|
Design by
v6.00.203 © 2003-2005
|
Design by 