|
Zadanie 1.
Pociąg jadący z prędkością 75 wjeżdża do tunelu o długości 2,5 km. Długość pociągu wynosi 250 m. Ile czasu pociąg będzie przejeżdżać przez tunel? wjeżdża do tunelu o długości 2,5 km. Długość pociągu wynosi 250 m. Ile czasu pociąg będzie przejeżdżać przez tunel?
Zadanie 2.
Dane są odcinki o długościach k i l. Skonstruuj odcinek długości d, gdzie d=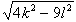 . Kiedy taki odcinek istnieje? . Kiedy taki odcinek istnieje?
Zadanie 3.
W trapezie prostokątnym ABCD przedłużono jego ramiona aż do przecięcia się w punkcie E. Oblicz długości odcinków DE i AE, jeżeli: |AB| = 8, |AD| = 4, |CD| = 6.
Zadanie 4.
Pewien przedsiębiorca posiada 2 hale fabryczne zbudowane na planie zacieniowanego ob-szaru, o łącznej powierzchni 100 m2. Hala nr 2 ma kształt kwadratu. Właściciel gruntu zaofe-rował przedsiębiorcy parcelę (A). Wówczas miałby on dwie hale, obydwie na planie kwadratu. Wysokość każdej hali byłaby równa jej długości. Jaką łączną kubaturę miałyby obydwie hale, każda w kształcie sześcianu, z płaskim dachem?

Zadanie 5.
Marek i Kuba byli bardzo głodni. Marek zamówił więc sobie pizzę "Monika", która miała 40 cm średnicy, a Kuba zamówił pizzę "Italiana", która miała aż 60 cm średnicy. Niestety, Marek był w stanie zjeść tylko 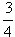 potrawy, a Kuba potrawy, a Kuba 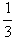 . Który z chłopców zjadł więcej i o ile? . Który z chłopców zjadł więcej i o ile?
Zadanie 6.
.gif) jest liczbą niewymierną. Jej przedstawienie w postaci ułamka dziesiętnego jest nieskoń-czone i nieokresowe. Z dokładnością do sześciu miejsc po przecinku jest ono równe 2,236068. Znajdź przybliżoną wartość jest liczbą niewymierną. Jej przedstawienie w postaci ułamka dziesiętnego jest nieskoń-czone i nieokresowe. Z dokładnością do sześciu miejsc po przecinku jest ono równe 2,236068. Znajdź przybliżoną wartość  bez kalkulatora (z dokładnością do trzech miejsc po przecinku). bez kalkulatora (z dokładnością do trzech miejsc po przecinku).
Zadanie 7.
Dana jest prosta l i punkt M nie należący do niej. Uzupełnij rysunek jednym punktem P w ten sposób, aby figura złożona z prostej i dwóch punktów miała środek symetrii. Jaką figu-rę tworzą wszystkie punkty P spełniające dany warunek? Odpowiedź uzasadnij.
Zadanie 8.
Dla jakich wartości x i y punkty: A = (2x-3y+1; y-x+3) i A1 = (4y-5x+2; 2x-y) są symetryczne względem osi OY?
Zadanie 9.
Na poniższym rysunku proste a, b są równoległe, natomiast prosta d zawiera dwusieczną kąta utworzonego przez proste c, b. Wiadomo, że prosta a tworzy z prostą c kąt o mierze 50�. Jaką miarę ma kąt x? Odpowiedź uzasadnij.

POWODZENIA!
|

![]](themes/crookedgreen/images/whiter.gif)
 v6.00.203 © 2003-2005
|
Design by
v6.00.203 © 2003-2005
|
Design by 