Zadanie 1.

A) Czy następujące lata są przestępne: 1956, 1997, 1900, 2000? Odpowiedź uzasadnij.
B) Podaj datę ostatniego dnia XX wieku.
C) Podaj datę dnia poprzedzającego 1 stycznia 1 r. n. e.

Zadanie 2.
Na trójkącie równoramiennym o rozwartości ramion 100° opisano okrąg. Średnica okręgu i podstawa trójkąta są podstawami trapezu wpisanego w ten okrąg. Oblicz miary kątów trapezu.

Zadanie 3.
Dla jakich liczb całkowitych a i b funkcje x 2x + b i x ax + 3 (a 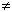0) mają to samo miejsce zerowe?

Zadanie 4.
Dany jest trójkąt równoramienny ABC. Przez dowolny punkt D (D ą A i D ą B) należący do podstawy trójkąta poprowadzono proste prostopadłe do ramion AC i BC, które przecinają je odpowiednio w punktach E i F. Udowodnij, że wysokość poprowadzona do jednego z ramion danego trójkąta ma długość |DE| + |DF|.

Zadanie 5.
Dwóch robotników miało wykonać pewną partię śrub. Gdy pierwszy pracował 7 godzin, a drugi 4 godziny, okazało się, że wykonali razem 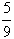całej pracy. Następnie pracowali razem jeszcze przez 4 godziny i ustalili, że pozostało im do wykonania całej pracy. W ciągu ilu godzin każdy z nich mógłby wykonać całą partię śrub samodzielnie?

POWODZENIA!