|
Zadanie 1.
Za pomocą odcinków równoległych do przekątnych kwadratu i jednego odcinka równoległego do boku można kwadrat podzielić na 7 części, z których można układać różne kształty. Punkty S i T są środkami boków kwadratu, punkt O jego środkiem symetrii.
A) |
B) |
Figury przestawione na rysunkach A i B otrzymano układając niektóre części kwadratu o boku 10 cm, podzielonego tak, jak na rysunku powyżej. Ustal, które części kwadratu wykorzystano do ułożenia figur, a następnie oblicz pole powierzchni każdej z figur A i B.
Zadanie 2.
Jest godzina 1500. Ile czasu upłynie do momentu, gdy wskazówki zegara pokryją się ze sobą po raz pierwszy?
Zadanie 3.
Dana jest funkcja, która długości podstawy trójkąta równoramiennego o obwodzie 26 cm przyporządkowuje długość ramienia tego trójkąta:
- podaj wzór tej funkcji,
- wyznacz jej dziedzinę,
- narysuj wykres funkcji w układzie współrzędnych.
Zadanie 4.
Średnia arytmetyczna liczb x i y jest równa  . Ile wynosi 
Zadanie 5.
Oblicz pole i obwód sześciokąta foremnego wiedząc, że różnica między długością dłuższej i krótszej przekątnej
wynosi 2 cm.
Zadanie 6.
Udowodnij, że kwadrat dowolnej liczby nieparzystej zmniejszony o 1 jest podzielny przez 8.
Zadanie 7.
Oblicz wartości wyrażeń i odpowiedz na zadane pytania. Następnie wykreśl z tabelki litery odpowiadające uzyskanym rozwiązaniom. Pozostałe litery utworzą hasło. Zapisz dokładnie wszystkie obliczenia i otrzymane hasło.
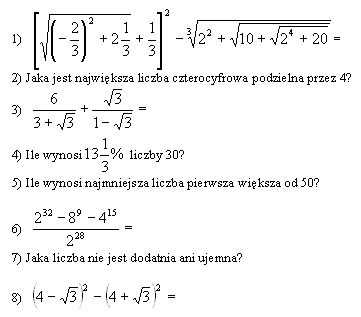
POWODZENIA!
|
![]](themes/crookedgreen/images/whiter.gif)
v6.00.203 © 2003-2005
|
Design by 