|
Zadanie 1.
Dany jest prostopadłościan o długościach krawędzi: a, b, c. Oblicz pole powierzchni tego prostopadłościanu, jeżeli:
- a jest rozwiązaniem równania:

- b jest wartością wyrażenia:
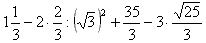
- c jest współczynnikiem kierunkowym prostej:
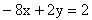
Zadanie 2.
Z papierowego krążka, o polu 9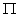 , wycięto współśrodkowo mniejszy krążek. Powstały pierścień ma pole 5 , wycięto współśrodkowo mniejszy krążek. Powstały pierścień ma pole 5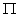 . Oblicz szerokość pierścienia. . Oblicz szerokość pierścienia.
Zadanie 3.
Jan dał Pawłowi 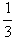 swoich pieniędzy, następnie Paweł dał Andrzejowi swoich pieniędzy, następnie Paweł dał Andrzejowi  wszystkich pieniędzy, które miał po otrzymaniu pieniędzy od Jana, następnie Andrzej dał Janowi wszystkich pieniędzy, które miał po otrzymaniu pieniędzy od Jana, następnie Andrzej dał Janowi 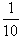 wszystkich pieniędzy, które miałpo otrzymaniu pieniędzy od Pawła. Ostatecznie każdy miał po 90 zł. wszystkich pieniędzy, które miałpo otrzymaniu pieniędzy od Pawła. Ostatecznie każdy miał po 90 zł.
Ile pieniędzy miał każdy z nich na początku?
Zadanie 4.
Kwadrat i romb mają równe obwody.
Który z tych wielokątów ma większe pole i dlaczego?
Zadanie 5.
Zbadaj, czy istnieje ostrosłup, w którym liczba wszystkich krawędzi jest o 5 większa od liczby wszystkich wierzchołków.
Zadanie 6.
Każde dwa wierzchołki sześciokąta foremnego połączono odcinkiem zielonym lub czerwonym. Wykaż, że został narysowany, co najmniej, jeden trójkąt o bokach tego samego koloru.
UWAGA: Do zadań 1, 3, 4, 5, 6 wykonaj rysunki.
|

![]](themes/crookedgreen/images/whiter.gif)
 v6.00.203 © 2003-2005
|
Design by
v6.00.203 © 2003-2005
|
Design by 