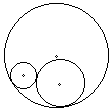
Dwa okręgi styczne zewnętrznie są równocześnie styczne wewnętrznie do trzeciego okręgu o promieniu długości 3 cm, tak jak na rysunku. Oblicz obwód trójkąta, którego wierzchołkami są środki tych okręgów.
Zadanie 1.
Wyraź 10 za pomocą pięciu dziewiątek. Podaj trzy różne sposoby. Uwaga: możesz używać znaków działań arytmetycznych.
Zadanie 2.
Dwa okręgi styczne zewnętrznie są równocześnie styczne wewnętrznie do trzeciego okręgu o promieniu długości 3 cm, tak jak na rysunku. Oblicz obwód trójkąta, którego wierzchołkami są środki tych okręgów.

Zadanie 3.
Spośród poniższych zdań, wskaż zdanie będące definicją rombu.
Zadanie 4.
Znajdź resztę z dzielenia liczby 299 przez 3.
Zadanie 5.
Drewniany sześcian, którego wszystkie ściany są pomalowane na czerwono, został rozpiło-wany na 1000 przystających sześcianów. Ile jest sześcianów, które:
Zadanie 6.
Oblicz pole figury zakropkowanej na rysunku,

wiedząc, że |AB| = 2a, |BC| = a, gdzie a > 0 oraz E i F są środkami boków AB i CD prostokąta ABCD.
Zadanie 7.
Wśród dziewięciu monet znajduje się dokładnie jedna moneta fałszywa, która jest minimal-nie lżejsza od pozostałych. Iloma ważeniami, nie używając odważników, można wykryć monetę fałszywą, jeżeli do dyspozycji mamy wagę szalkową? Opisz przebieg ważenia.
Zadanie 8.
Dane są trójkąty o bokach długości:
Zadanie 9.
Odtwórz brakujące cyfry:
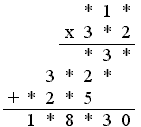
POWODZENIA!