Jaką liczbę należy wpisać w pustą kratkę w równaniu: 5 (
 + 3 x) (x + 1) - 4 (1 + 2 x)2 = 80, jeżeli wiadomo, że liczba 2 jest rozwiązaniem tego równania?
+ 3 x) (x + 1) - 4 (1 + 2 x)2 = 80, jeżeli wiadomo, że liczba 2 jest rozwiązaniem tego równania?
Zadanie 1.
Jaką liczbę należy wpisać w pustą kratkę w równaniu: 5 ( + 3 x) (x + 1) - 4 (1 + 2 x)2 = 80, jeżeli wiadomo, że liczba 2 jest rozwiązaniem tego równania?
+ 3 x) (x + 1) - 4 (1 + 2 x)2 = 80, jeżeli wiadomo, że liczba 2 jest rozwiązaniem tego równania?
Zadanie 2.
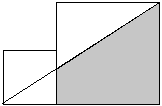
Dane są dwa kwadraty o bokach 3 dm i 5 dm, położone jak na rysunku. Wyznacz stosunek pól zacieniowanej części dużego kwadratu i tego kwadratu.
Zadanie 3.
Jaka jest cyfra jedności liczby a, jeśli 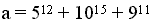 ?
?
Zadanie 4.
Kozę przywiązano do rogu chałupy stojącej w środku dużej łąki. Wyznacz pole obszaru, po którym może poruszać się koza (skubiąc trawę), jeśli chata ma wymiary 4 m x 6 m, a długość postronka, na którym uwiązano kozę, wynosi 9 m.

Zadanie 5.
W zbiorze liczb całkowitych określamy działanie  w ten sposób, że a
w ten sposób, że a  b = a b + a + b np.:
b = a b + a + b np.:
2  3 = 2 × 3 + 2 + 3
3 = 2 × 3 + 2 + 3
2  3 = 6 + 5
3 = 6 + 5
2  3 = 11
3 = 11
Oblicz x wiedząc, że 2  x = 3
x = 3  5.
5.
Zadanie 6.
Z załączonych klocków zbuduj sześcian. Złożony model pokaż komisji przy oddawaniu pracy.
Zadanie 7.
Znajdź błąd w poniższym "dowodzie".
Każda liczba równa się swojej połowie
Wiadomo, że:
(a + b) (a - b) = a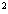 - b
- b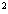 .
.
Równość ta jest prawdziwa także w przypadku, gdy a = b. Wówczas:
(a + a) (a - a) = a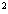 - a
- a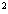 .
.
Prawą stronę tego równania możemy tak napisać:
(a + a) (a - a) = a (a - a)
Obie strony dzielimy przez (a - a) i otrzymujemy
a + a = a, czyli 2 a = a, skąd a = 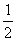 a.
a.
Zadanie 8.
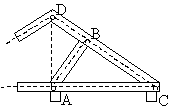
Rodzice Alicji budują na działce rekreacyjnej domek letniskowy (rysunek poniżej). Zaprojektowano następujące wiązania dachu: belka AB jest prostopadła do belki CD. Mając dane |CD| = 5 m i |AC| = 4 m, oblicz długość belki AB.
POWODZENIA!