Dla jakiego x wartość liczbowa wyrażenia
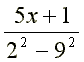
będzie liczbą mniejszą od zera?
Zadanie 1.
Dla jakiego x wartość liczbowa wyrażenia 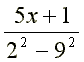
będzie liczbą mniejszą od zera?
Zadanie 2.
Długość prostokąta ABCD wynosi 2 dm, a jego szerokość - 9 cm. Oblicz pole trójkąta APC, gdzie punkt P jest środkiem boku BC.
Zadanie 3.
W pierwszym roku po posadzeniu roślina wypuszcza jedną gałązkę, a w każdym następnym roku liczba jej gałązek podwaja się. Na każdej z gałęzi zakwitają dwa kwiaty.
a) Oblicz, ile gałązek i kwiatów będzie miała roślina po sześciu latach.
b) Podaj zależności, które pozwolą Ci wykonać obliczenia po upływie x lat.
Zadanie 4.
Narysuj trójkąt ABC o wierzchołkach: A = (-2; -3), B = (-5; 1), C = (2:1), a następnie znajdź jego obrazy w symetrii osiowej względem osi x oraz w symetrii względem osi y. Jaką figurą jest część wspólna obrazów trójkąta ABC w symetrii względem osi x oraz osi y? Czy posiada ona oś symetrii, środek symetrii? Jeśli tak, to zaznacz je na rysunku.
Zadanie 5.
Rodzice oferują Ci wybór między dwoma wariantami obliczania kieszonkowego.
I wariant: Początkowo 600 zł rocznie z podwyżką o 30 zł co 12 miesięcy.
II wariant: Początkowo 300 zł półrocznie z podwyżką o 7,50 zł co 6 miesięcy.
Który z wariantów gwarantuje Ci większe wypłaty? Odpowiedź uzasadnij.
Zadanie 6.
Czy można zbudować siatkę ostrosłupa prawidłowego czworokątnego, jeśli przekątna podstawy miałaby długość 20 cm, a krawędź boczna 10 cm? Odpowiedź uzasadnij.
Zadanie 7.
Zamień ułamek dziesiętny okresowy 0,42(5) na ułamek zwykły.
Zadanie 8.
Która z liczb "zakłóca" porządek?
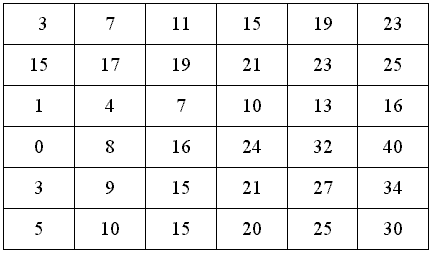
POWODZENIA!