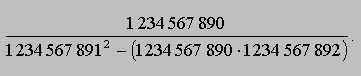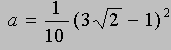...::: Złota Żaba - matematyka - etap II - 2001/02 :::...
Dodane przez administracja dnia 05.10.2005 17:26
Zadanie 1.
Rozmaitości:
A. Dla jakich wartości k i n punkty A = (3 - 2k, 1) oraz A? = (5, -3n + 3) są symetryczne względem osi odciętych x?
B. Do równania 3x + y = 1 dopisz drugie równanie tak, aby otrzymać układ:
- oznaczony (układ równań niezależnych),
- sprzeczny.
C. Ile centymetrów kwadratowych mieści się w kilometrze kwadratowym? Odpowiedź zapisz w postaci potęgi liczby 10.
D. Oblicz wartość wyrażenia:
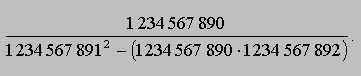
Zadanie 2.
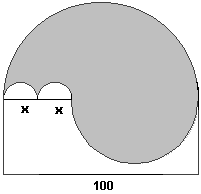
Napisz wzór na obliczanie pola oraz wzór na obliczanie obwodu zacieniowanej figury w zależności od x (brzegiem zacieniowanej figury są cztery półokręgi). Ustal, dla jakich x zadanie ma sens.
Zadanie 3.
W Stanach Zjednoczonych temperaturę mierzy się w stopniach Fahrenheita. Jeśli temperaturę w skali Celsjusza oznaczymy literą C, a temperaturę w skali Fahrenheita literą F, to temperaturę w skali Fahrenheita można obliczyć ze wzoru A. Jaka jest temperatura w skali Fahrenheita, gdy w skali Celsjusza jest 100°?
A. Jaka jest temperatura w skali Fahrenheita, gdy w skali Celsjusza jest 100°?
B. Jaka jest temperatura w skali Celsjusza, gdy w skali Fahrenheita jest 50°?
C. Termometr posiada skalę Celsjusza i Fahrenheita. Przy jakiej temperaturze termometr wskaże
w obu skalach tę samą liczbę?
Zadanie 4.
Ze 125 jednakowych kulek z modeliny o promieniu długości 2 cm ulepiono jedną kulę. Oblicz długość promienia otrzymanej kuli.
Zadanie 5.
Oblicz pole czworokąta ograniczonego prostymi o równaniach: y = -1, y = 3, y = x + 5, y = -2x + 7 (długości potrzebnych odcinków odczytaj z rysunku).
Zadanie 6.
Porównaj liczby:
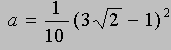
i

Zadanie 7.
Dany jest trójkąt prostokątny ABC, gdzie miara kąta |ABC| = 90°. Z wierzchołka kąta prostego poprowadzono środkową BD oraz wysokość BE. Wykaż, że kąt utworzony przez wysokość i krótszą przyprostokątną jest przystający do kąta utworzonego przez środkową i drugą przyprostokątną.
(Środkową trójkąta nazywamy odcinek łączący wierzchołek trójkąta ze środkiem przeciwległego boku).
Zadanie 8.
W skokach narciarskich w każdej serii sumuje się dla zawodnika punkty za długość skoku i punkty przyznane przez komisję sędziowską.
Punkty za długość skoku obliczane są w następujący sposób: za lądowanie w punkcie K zawodnik otrzymuje 60 punktów, każdy metr dalej daje dodatkowo 1,8 punktu, a za wylądowanie przed punktem K traci się 1,8 punktu na metrze (długość skoku mierzy się z dokładnością do pół metra). Styl lotu i lądowanie oceniane są przez pięciu sędziów. Każdy sędzia może przyznać od 0 do 20 punktów (z dokładnością do 0,5 pkt). Odrzuca się dwie skrajne noty i sumuje punkty przyznane przez trzech pozostałych sędziów.
Podczas zawodów skoczek zdobywa tyle punktów, ile w sumie otrzyma ich w dwóch seriach skoków.
W tabeli przedstawiono wyniki skoków dwóch najlepszych zawodników:
|
długość
skoku
|
noty
sędziów
|
|
1
|
2
|
3
|
4
|
5
|
|
Adam
Małysz
|
I
seria
|
129,0
m
|
19,5
|
19,0
|
19,0
|
19,5
|
19,0
|
|
II
seria
|
131,5
m
|
19,5
|
19,5
|
20,0
|
19,5
|
19,5
|
|
Sven
Hannavald
|
I
seria
|
134,5
m
|
19,5
|
19,0
|
19,0
|
19,0
|
19,0
|
|
II
seria
|
128,0
m
|
18,0
|
18,5
|
18,5
|
18,0
|
18,0
|
Punkt K znajduje się na 120 metrze.
Ile punktów zdobył Małysz, a ile Hannavald? Który z nich zwyciężył?
P O W O D Z E N I A !
 A. Jaka jest temperatura w skali Fahrenheita, gdy w skali Celsjusza jest 100°?
A. Jaka jest temperatura w skali Fahrenheita, gdy w skali Celsjusza jest 100°?