Sześcian ma osiem narożników. Każdy z nich ścinamy w ten sposób, że krawędzie wychodzące z danego wierzchołka zostaną przecięte w
 długości. Ile wierzchołków, krawędzi i ścian ma bryła, która powstała po odrzuceniu narożników?
długości. Ile wierzchołków, krawędzi i ścian ma bryła, która powstała po odrzuceniu narożników?
Zadanie 1.
Przy dzieleniu liczby 4373 przez liczbę naturalną n otrzymujemy resztę 8, przy dzieleniu zaś liczby 826 przez n otrzymujemy resztę 7. Znajdź n.
Zadanie 2.
Sześcian ma osiem narożników. Każdy z nich ścinamy w ten sposób, że krawędzie wychodzące
z danego wierzchołka zostaną przecięte w  długości. Ile wierzchołków, krawędzi i ścian ma bryła, która powstała po odrzuceniu narożników?
długości. Ile wierzchołków, krawędzi i ścian ma bryła, która powstała po odrzuceniu narożników?
Zadanie 3.
W bieżącym roku Tim Montgomery pobił rekord świata w biegu na 100 m, uzyskując czas 9,72 s. Oblicz średnią prędkość sprintera w tym biegu wyrażoną w km/h . Wynik podaj z dokładnością do części setnych.
Zadanie 4.
Oblicz pole pierścienia utworzonego przez dwa współśrodkowe okręgi wiedząc, że odcinek AB leży na stycznej do mniejszego okręgu, jego końce należą do okręgu o większym promieniu
i długość tego odcinka wynosi 10 cm.
Zadanie 5.
Liczba 2002 jest palindromem, tzn. że czyta się ją tak samo od lewej jak i prawej strony.
Zadanie 6.
Narysuj figury, których pola można opisać wzorami:
Zadanie 7.
Masa słupa powietrza wywierającego nacisk na 1 cm2 powierzchni Ziemi wynosi 1 kg. Oblicz masę (w tonach) warstwy powietrza otaczającego Ziemię. Przyjmij, że powierzchnia Ziemi wynosi 510 milionów km2.
Zadanie 8.
Rysunek przedstawia fragment okna oraz oś symetrii okna.
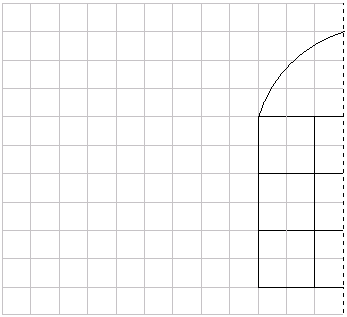
W ścianie frontowej budowli znajdują się cztery okna (fragment jednego z nich przedstawiono na rysunku powyżej), drzwi wejściowe, które swym kształtem przypominają kształt okna, ale jego wymiary są dwa razy większe od wymiarów okna oraz rozeta, której średnica jest równa  szerokości okna. Osią symetrii tej ściany jest oś symetrii drzwi, która jest równoległa do osi symetrii okien. W prostokącie o bokach 20 cm x 14,5 cm zaplanuj rozmieszczenie opisanych elementów przyjmując, że szerokość okna wynosi 3 cm i pierwsze dwa okna znajdują się 3 cm od podstawy prostokąta, a odstępy między tymi oknami a drzwiami wynoszą 1,5 cm. Pozostałe okna umieszczono 1,5 cm nad dolnymi oknami, w odległości 5,5 cm od osi symetrii ściany. Środek rozety leży na osi symetrii ściany w odległości 3 cm od górnej części drzwi.
szerokości okna. Osią symetrii tej ściany jest oś symetrii drzwi, która jest równoległa do osi symetrii okien. W prostokącie o bokach 20 cm x 14,5 cm zaplanuj rozmieszczenie opisanych elementów przyjmując, że szerokość okna wynosi 3 cm i pierwsze dwa okna znajdują się 3 cm od podstawy prostokąta, a odstępy między tymi oknami a drzwiami wynoszą 1,5 cm. Pozostałe okna umieszczono 1,5 cm nad dolnymi oknami, w odległości 5,5 cm od osi symetrii ściany. Środek rozety leży na osi symetrii ściany w odległości 3 cm od górnej części drzwi.
Zadanie 9.
Do ponumerowania stron pewnej książki użyto 1830 czcionek przedstawiających cyfry. Ile stron liczy ta książka?
Zadanie 10.
Narysuj dowolny trapez, a następnie wykreśl trójkąt o tym samym polu. Uzasadnij rozwiązanie.
POWODZENIA!