Zadanie 1.
Rozwiąż krzyżówkę. Podaj, ile razy występują w krzyżówce następujące litery: a, g, r.

Zadanie 1.
Rozwiąż krzyżówkę. Podaj, ile razy występują w krzyżówce następujące litery: a, g, r.

Zadanie 2.
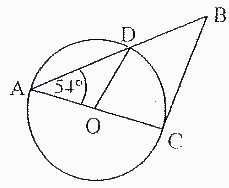
Oblicz kąty czworokąta OCBD, jeśli kąt BAC ma miarę 54° i odcinki AC oraz BC są równej długości.
Zadanie 3.
Zadanie 4.
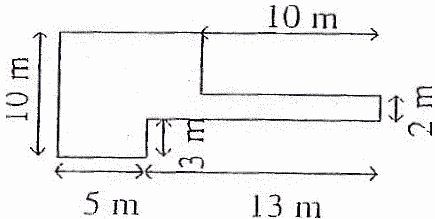
Oblicz obwód i pole figury przedstawionej poniżej:
Zadanie 5.
Na jednej szalce położono dwie jednakowe tabliczki czekolady, na drugiej 2/5 takiej tabliczki i 32 dag. Nastąpiła równowaga. Ile waży tabliczka czekolady?
Zadanie 6.
Wiadomo, że w kwadracie przekątne są równej długości i są do siebie prostopadłe. Czy prawdą jest, że czworokąt, w którym przekątne są równe i do siebie prostopadłe, jest kwadratem? Odpowiedź uzasadnij.
Zadanie 7.
Uzupełnij działania cyframi, aby obliczenia były prawidłowe.

Zadanie 8.
Rozstrzygnij, które z poniższych figur przedstawiają siatki sześcianu.
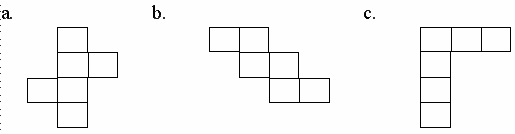

POWODZENIA!